t検定で必要なサンプルサイズを求める方法

A/Bテスト実践ガイドという本を読んでいたら、有意水準5%、検出力80%のt検定に必要なサンプルサイズを求める公式として以下のようなものが書かれていました

$$n = \frac{16\sigma^2}{\delta^2}.$$

ここで$\sigma$は分散（両群で等しいとする）、 $\delta$ は検出したい二群の平均の差です。この式がどこから出てくるのかパッとわからなかったので考えました。

用語ですが

• 有意水準5%とは、帰無仮説が真である時に帰無仮説を棄却する誤りを犯す確率が5%
• 検出力80%とは、帰無仮説が偽である時に帰無仮説を棄却できる確率が80%

ということです。両者はトレードオフの関係にあります。実験を設定する時には、検出したい差の大きさ $\delta$ を検出できる（差が$\delta$の時に高い確率で帰無仮説を棄却できる）ようなサンプルサイズを確保することが求められます。この辺をちゃんと分析していないと、A/Bテストをやってみて有意差が出なかったが、それが本当に差がなかったからなのか、単にサンプルサイズが足りなかったからなのかという点が区別できません。なので実験前に期待される差の大きさと分散から必要なサンプルサイズを見積もっておく必要があるわけです。

上の式の話に戻ります。二群の平均の差に関するt検定なので

$$ t = \frac{\delta}{\sigma}\sqrt{\frac{n}{2}}$$

を考えることになります。サンプル数は両群で等しいとします。有意水準5%で帰無仮説を棄却できないのは $|t|<1.96$ となるときです。 帰無仮説が偽 ($ \delta \cancel= 0 $) のときに得られた $t$ がこの領域に入ってしまうと、「帰無仮説が偽であるときに帰無仮説を棄却しない」誤りを犯すことになります。 検出力80%という意味はこの誤りの確率を20%以下にするということです。標準正規分布の上側20%点は0.84なので、

$$ t = \frac{\delta}{\sigma}\sqrt{\frac{n}{2}} > 1.96 + 0.84 $$

であれば求める検出力を達成できることになります。図にすると以下のような感じです

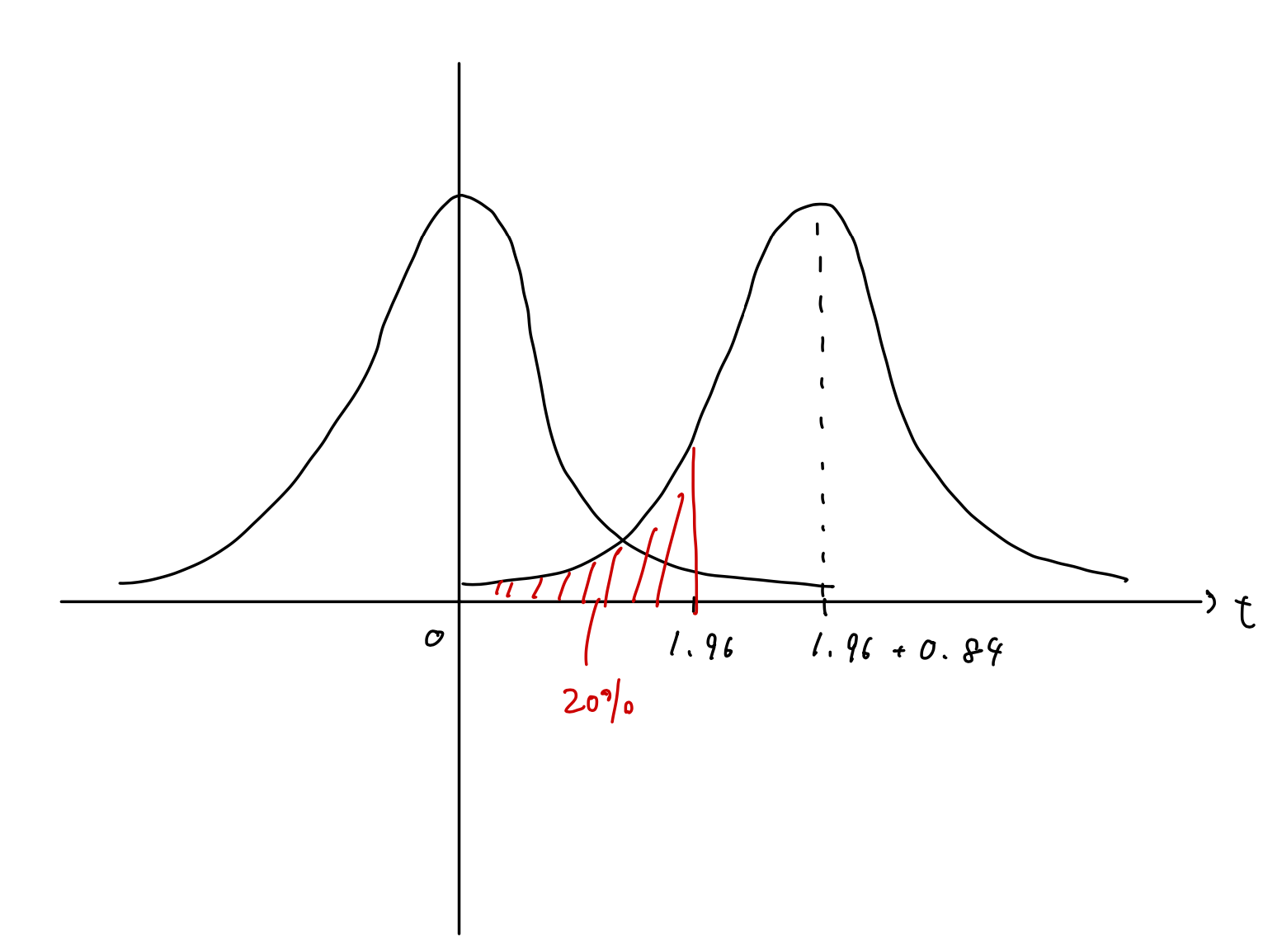
多くのケースでは検出したい差の大きさ（効果量）$\delta$ を定めて必要な $n$ を計算することになると思います。なので必要なサンプルサイズは最低でも

$$ n = 2(1.96 + 0.84)^2\frac{\sigma^2}{\delta^2} \simeq \frac{16\sigma^2}{\delta^2} $$

となります。