モデルが生成したデータを学習に繰り返し使うとどうなるか

#model-collapse

2023-06-28

The Curse of Recursion: Training on Generated Data Makes Models Forget という論文が Import AI で紹介されていて面白かったのでざっくり自分でも確かみてみた。

内容としては、モデルが生成したデータを別のモデルの学習に使うということを繰り返していくと、次第に分布の tail の情報が失われていって、出力の範囲が狭まってしまうという指摘。特に生成AIの結果がインターネットに溢れ始めた昨今では重要になってくるはず。

論文では混合ガウス分布等を例に取って、理論解析と数値解析をしており、この現象を model collapse と呼んでいる。数値解析の方は簡単にできそうだったので自分でも実装してみた。

Python 実装

やりたいことは、一次元の混合ガウス分布のパラメータフィットをして、フィットされた分布から新しくデータを生成し、それを元に分布を再びフィットするということを何度も繰り返すことだ。

具体的には、第 $i$ ステップの学習データがある時に、以下三つを混ぜて第 $i+1$ ステップの学習データを構成する

第 $i$ ステップにおける学習データ
第 $i$ ステップの学習データを使ってフィットした混合ガウス分布からのサンプル
真の分布からのサンプル

$i=0$ では真の混合ガウス分布からのサンプルとし、三つのデータの比率は適当に変えて良い。Python で実装すると、以下の sample_next_gen 関数のようになる:

from collections import namedtuple
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from tqdm import tqdm

GaussianMixtureParams = namedtuple('GaussianMixtureParams', ('mus', 'sigmas', 'mixture_ratio'))

def sample_from_gaussian_mixture(gm_params, num_samples):
    mus = np.array(gm_params.mus)
    sigmas = np.array(gm_params.sigmas)

    num_mixture = len(gm_params.mixture_ratio)
    mixture_idx = np.random.choice(num_mixture, size=num_samples, p=gm_params.mixture_ratio)
    standard_normal_noises = np.random.normal(size=num_samples)
    samples = mus[mixture_idx] + standard_normal_noises * sigmas[mixture_idx]

    return samples

def fit_gaussian_mixture(samples, n_components, random_state=0):
    gm = GaussianMixture(n_components=n_components, random_state=random_state).fit(samples.reshape(-1,1))

    mus = gm.means_.reshape(-1)
    sorted_idx = np.argsort(mus)

    gm_params = GaussianMixtureParams(
        gm.means_.reshape(-1)[sorted_idx],
        np.sqrt(gm.covariances_).reshape(-1)[sorted_idx],
        gm.weights_[sorted_idx]
    )

    return gm_params


def sample_next_gen(gm_params_org, gm_params_fitted, samples_current_gen, ratio_org, ratio_fitted, num_samples):
    # オリジナルの分布、フィットされた分布、最新のサンプルからのサンプリングを使う
    num_samples_org = int(num_samples * ratio_org)
    num_samples_fitted = int(num_samples * ratio_fitted)
    num_samples_current = num_samples - num_samples_org - num_samples_fitted
    if num_samples_current < 0:
        raise ValueError("Invalid ratio")

    samples_org = sample_from_gaussian_mixture(gm_params_org, num_samples_org)
    samples_fitted = sample_from_gaussian_mixture(gm_params_fitted, num_samples_fitted)
    samples_current = np.random.choice(samples_current_gen, size=num_samples_current, replace=False)

    return np.concatenate([samples_org, samples_fitted, samples_current])

結果

各回 $N=10000$ のサンプリングを合計2000ステップ実行してみた。真の混合ガウス分布は component 二つでパラメータは

$\boldsymbol \mu = (-2, 2)$
$\boldsymbol \sigma = (1, 1)$
混合比 1:1

とした。簡単のため、学習データは全て前回ステップでフィットした分布から生成した。

num_samples = 10000
num_gen = 2000

gm_params_org = GaussianMixtureParams([-2, 2], [1, 1], [0.5, 0.5])
samples = sample_from_gaussian_mixture(gm_params_org, num_samples)

for _ in tqdm(range(num_gen)):
    gm_params_fitted = fit_gaussian_mixture(samples, 2)
    samples = sample_next_gen(gm_params_org, gm_params_fitted, samples, 0.0, 1.0, num_samples)

フィットされた分散の推移をプロットしてみると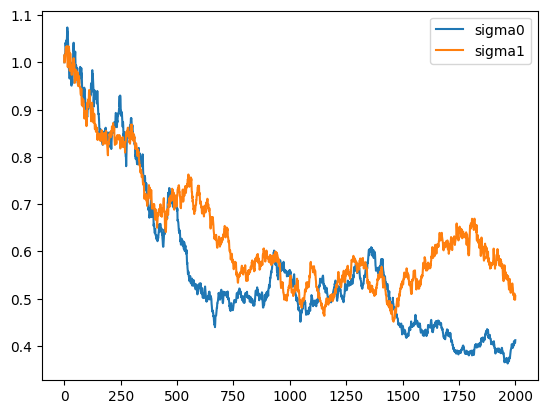となり確かにより狭い分布に向かっている様子がわかる。

また初回のヒストグラムと、2000ステップ目でのヒストグラムを比較してみると、混合比も片方の山に偏っていっているように見える。

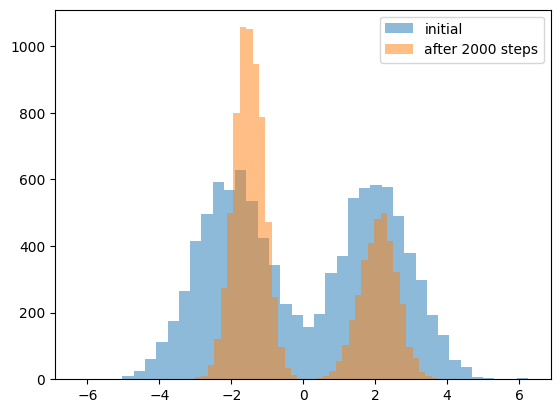
ただ、乱数シードを変えて何回か繰り返したところフィットされた分布がより広い方向に向かうこともあったし、三種類のデータの混合比によって model collapse の速度も変わったりした。どれくらい現実のLLMなどに当てはまる結果なのかはわからない。

ノートブックへのリンクはこちら。間違いがあったら教えてください。