ランキングモデルのポジションバイアスに対処する
はじめに
最近KDD2023の論文を読んでいたのですが、その中で以下の論文が目に留まりました。
Learning to rank におけるポジションバイアスに対処する手法の提案で、特に著者達が click modeling と呼ぶアプローチを発展させたものになっています。
今回はこの論文をベースにいくつかポジションバイアス除去系のモデルを実装して比較してみました。
Table of contents
ポジションバイアスの除去
推薦や検索ではユーザーがサービスを使う間に自然に発生するクリックなどのイベントを、機械学習のラベルとして用いることがよくあります。しかしこのようなイベントの発生は、単純なユーザーの嗜好だけではなく、そもそもサービス上でユーザーがそのアイテムを目にする機会があったかどうかにも左右されます。嗜好が同程度のアイテムであれば上位に表示された方がクリックされやすくなるため、ポジションの影響を考慮に入れないとモデルの推論結果にバイアスが乗ってしまうことになります。
バイアス除去の二つの方法
ランキング学習におけるポジションバイアスの除去はここ数年ホットな話題となっており、多くの論文が書かれているようです。冒頭の論文ではこれまで提案されてきた手法を大きく以下の二つに分類していました
- Counterfactual アプローチ: 傾向スコアによる重み付けを使うなど、counterfactual な分析手法の応用
- Click modeling アプローチ: アイテムのクリック確率を、アイテムの観測確率と、観測された上でクリックされる確率（CTR）に分解しモデリングする方法
Counterfactual アプローチ では傾向スコアを別途何らかの方法で入手・推定する必要があり、手間やコストがかかります。一方 click modeing アプローチは、サービスのログデータを使って通常のモデリングプロセスの枠内で実装できます。そのような手のつけやすさから産業界ではこちらがよく採用されるらしく、実際例えば Airbnb は click modeling アプローチを採用して実装したモデルの有効性を報告しています。
Click modeling のアイディア
Click modeling のアイディアはシンプルです。推薦や検索でユーザーにアイテムのリストを表示するような状況を念頭に起きます。ユーザー・アイテムペアを表す識別子を $i$ として変数を以下のように定義します。
- $c_i$: ユーザーがアイテムをクリックしたかを表す二値変数
- $o_i$: ユーザーがアイテムを観測したかを表す二値変数
- $\vec x_i$: ユーザー・アイテムの特徴量
一般にクリック確率は \begin{equation} \label{eq:eq-multi-rule} P(c_i=1|\vec x_i) = P(c_i=1|\vec x_i, o_i=1)\times P(o_i=1|\vec x_i) \end{equation}
と分解できます。ここで、$o_i=0$ ならば必ず $c_i=0$ になるとしました。
さらに特徴量 $\vec x_i$ が、以下のように分離できると仮定しましょう
- $\vec x_i^R$: ユーザーのアイテムに対する嗜好 (以下 relevance とも言います) のみに関係する特徴量。
- $\vec x_i^P$: アイテムの観測有無にのみ関係する特徴量。例えば、表示位置やデバイス情報。
つまり、式 \eqref{eq:eq-multi-rule} が以下のように書けるとします \begin{equation} \label{eq:eq-click-decompoese} P(c_i=1|\vec x_i) = P(c_i=1|\vec x_i^R, o_i=1)\times P(o_i=1|\vec x_i^P) \end{equation}
このようにクリック確率を、アイテムの観測確率と観測されたという条件付きでのクリック確率の積として表し、それぞれを異なる特徴量を持つ別のモデルとして表現するのが click modeling アプローチです。ユーザーの嗜好は第一項の $P(c_i=1|\vec x_i^R, o_i=1)$ で表されており、推論時にはこちらだけを使います。
PAL
PAL は click modeling アプローチの走りで、$P(c_i=1|\vec x_i^R, o_i=1)$ と $P(o_i=1|\vec x_i^P)$ をそれぞれニューラルネットワーク $r(\vec x_i^R)$ と $o(\vec x_i^P)$ で表し、以下のようなロス関数を使って学習することを提案しました \begin{align} \label{eq:pal-loss} L &= \frac{1}{N}\sum_{i=1}^N l(c_i, \psi_i) \\ \psi_i &= r(\vec x_i^R)o(\vec x_i^P)\notag \end{align} ここで $l$ はクロスエントロピーです。推論時には $r(\vec x_i^R)$ だけを用いることで、ポジションの影響を取り除いたユーザーの嗜好を予測することができます。
式 \eqref{eq:eq-click-decompoese} を見ると上記の積の形が自然に思えますが、冒頭の論文で引用されている様子を見ると $\psi_i=\mathrm{sigmoid}(r(\vec x_i^R)+o(\vec x_i^P))$ という和の形を採用することもあるようです。1
また冒頭の論文ではこのようなモデルを two tower model、 $r(\vec x_i^R)$ を relevance tower, $o(\vec x_i^P)$ を observation tower と呼んでいます。2
Relevance による交絡
PAL はポジションの影響を $o(\vec x_i^P)$ だけに押し付けるという発想ですが、式 \eqref{eq:pal-loss} のように単に特徴量を分割して積や和の形にモデルを書いただけでそう都合よくバイアスが緩和できるものなのでしょうか。
冒頭の論文では、PAL のような手法がうまくいくのはデータの観測構造が下図 (a) のようになっている時だと指摘しました（冒頭の論文より。$D$ が $\vec x^R$, $B$ が $o$, $P$ が $\vec x^P$ と思ってください）。
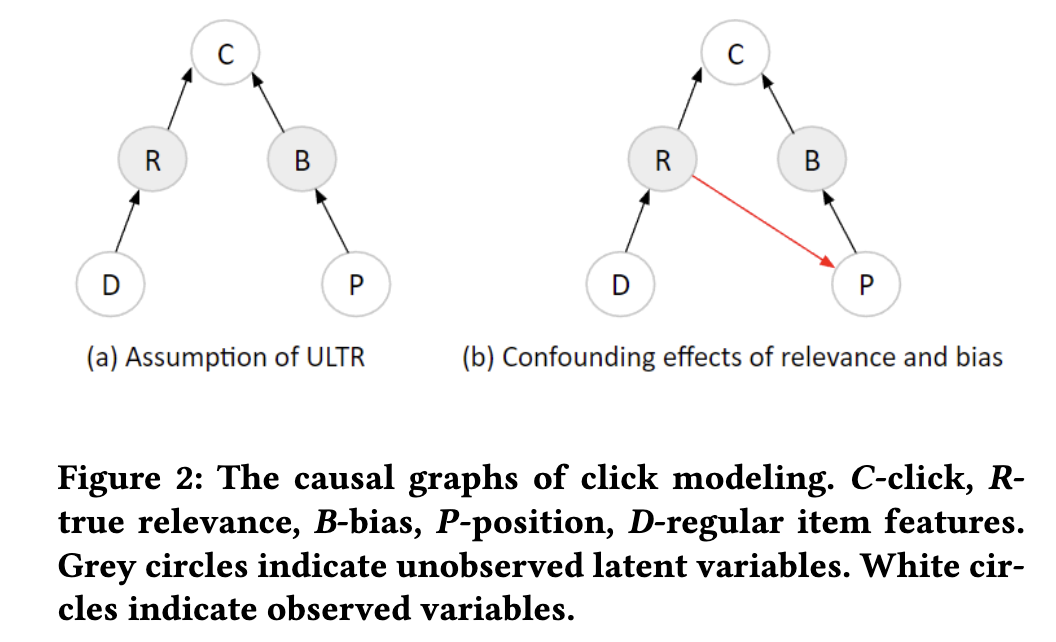
観測有無はポジションによってのみ決まり、relevance の影響は受けないという仮定になっています。
しかし実務では多くの場合、ログデータは過去のモデルの推論結果から生成されており、そのモデルはやはり relevance を学習しているため、(b) のように relevance がポジションとクリック両方の原因（交絡因子）になります。するとそのようなデータで学習したモデルは、relevance の学習のためにポジションを shortcut として利用できるようになってしまい、relevance tower にポジションの影響が入り込んでバイアスの除去を妨げてしまいます。
上記論文ではこの shortcut を緩和する手法として以下二つを提案していました。
Observation Dropout
これはその名の通り、observation tower $o(\vec x^P)$ に dropout を導入して、ポジションの shortcut を緩和します。ロス関数はこれまでと同じ式 \eqref{eq:pal-loss} です。
Gradient Reversal
この方法では、observation tower $o(\vec x^P)$ から relevance を unlearn します。具体的には式 \eqref{eq:pal-loss} に以下のロス関数を加えて joint で学習します。 \begin{equation} L_{rev}=\sum_i\left(y_i - \mathrm{Dense}(\mathrm{GradRev}(o(\vec x^P_i)))\right)^2 \end{equation} ここで $\mathrm{GradRev}$ は勾配の符号を反転させるレイヤーです (forward では何もしません）。$y_i$ は relevance のラベルで、ユーザーの真の嗜好を表しますが、通常は利用可能でないのでクリックラベルで代用したり、$r(\vec x^R)$ を使ったりすることが提案されています。
実験
冒頭の論文の提案手法も含めて、click modeling アプローチの効果を確かめる実験を行いました。基本的には論文に記載の手順に従いましたが、詳細が書かれていない部分も多くその場合は適当に想像して補っています。実装は以下に置いておきました。
クリックデータセットの生成
バイアス除去に関する実験をするには、バイアスの乗った学習データと、バイアスのないテストデータが必要になります。ここでは論文にならって、MSLR-WEB30K を加工してそのようなデータセットを作ることにします。MSLR-WEB30Kは Bing の検索から作った learning-to-rank 用のデータセットで、各クエリ・ドキュメントのペアに対して、136次元の特徴量ベクトルと、0-4 の relevance ラベル $y_i$ が付けられています。この $y_i$ をバイアスのない ground truth ラベルとします。
このデータセットにクリックの有無を表す二値ラベルを、以下の手順で人工的に付与します。
1. クエリごとにドキュメントのポジションを生成
各ドキュメントに以下で表されるスコア $s_i$ を生成し、クエリごとにその降順をドキュメントのポジション $p_i$ とします。 \begin{equation} s_i = wy_i + (1 - w)n_i,\text{ where } n_i \sim \mathrm{Uniform(0,4)} \end{equation}
スコアは relevance $y_i$ とランダムノイズの重み付き和で決まります。$w=1$ の時は完全に relevance によって決まり上で述べた交絡が強く発生しているという状況になります。逆に $w=0$ の時はポジションは relevance によらずランダムに決まり、交絡はありません。
2. ポジションに応じた人工クリックの生成
ポジションが上になるほど表示確率が高いという状況を \begin{equation} P(o_i=1|p_i) = \frac{1}{p_i} \end{equation}
と表現することにします。そして、$o_i=1$ の下でのクリック確率を \begin{equation} P(c_i=1|y_i, o_i=1)=\epsilon + (1-\epsilon)\frac{2^{y_i}-1}{2^{y_{\mathrm{max}}}-1} \end{equation}
とします。Relevance が高いほどクリックしやすく、また一定値のノイズ $\epsilon$ も付与されるという設定です。ここでは元論文にならい $\epsilon=0.1$ に固定します。
トータルのクリック確率はこの二つの積
$$ P(c_i=1|y_i,p_i)=P(c_i=1|y_i, o_i=1)\times P(o_i=1|p_i) $$
になります。MSLR-WEB30Kの各データに対して $P(c_i=1|y_i,p_i)$ に基づくベルヌーイ分布からサンプリングを行いました。
なお、この方法でクリックを生成すると正例 ($c_i=1$) が1%以下と不均衡が大きくなるため、以下の実験では負例を10%にダウンサンプリングして学習の効率化を図っています。
比較用のベースライン
比較のために、以下のベースラインを用意しました。
Linear model
目的変数を $c_i$ とする二値分類を、正則化項つきのロジスティック回帰で解きます。実装には scikit-learn を用いました。
またポジションバイアスを除去するため、学習時にポジションも特徴量として使い、推論時には一定値 ($p_i=1$) に固定するという方法も試しました (Debiased Linear)。これはGoogleのRules of machine learningにも紹介されている古典的なテクニックです。
GBDT
XGBoostの objective="rank:ndcg" でランキングモデルを作ります。またロジスティック回帰と同様に、ポジション特徴量を推論時に固定する方法も試しました（Debiased XGBoost）。3
Single Tower
目的変数を $c_i$ とする二値分類をMLPで解くモデルです。公平な比較をするため、two tower 系のモデルの relevance tower のパラメータ数は、この single tower と等しくなるようにしています。
Validation の方法
モデルのハイパーパラメータチューニングや early stopping などは、生成した人工クリックに基づく validation データを通して行いました。このクリックは本来最適化したい relevance に対してバイアスがあるわけですが、現実的な設定にしようと思うと多少バイアスが乗っていてもこれを使うしかありません（冒頭の論文にはこの辺の手法の詳細は書かれていませんでした）。
なお手元の計算リソースの都合上、パラメータチューニングといっても適当に手動で何パターンか試して良さそうなものに固定する、という程度のことしかしていません。
実験結果
以下に test データの relevance ラベルにおける、NDCG@5 を示します。バイアスのある人工クリックと異なり、これは真に評価したい unbiased な指標になります。
| w | linear | debiased_linear | xgboost | debiased_xgboost | single_tower | two_tower | obs_dropout | grad_rev |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.2787 | 0.3145 | 0.2683 | 0.1828 | 0.2658 | 0.3465 | 0.2860 | 0.3382 |
| 0.2 | 0.2851 | 0.3157 | 0.2964 | 0.1737 | 0.2983 | 0.3437 | 0.2984 | 0.3432 |
| 0.6 | 0.2935 | 0.3227 | 0.3057 | 0.2426 | 0.2436 | 0.3255 | 0.3434 | 0.3341 |
| 0.8 | 0.2957 | 0.3246 | 0.3124 | 0.1768 | 0.2924 | 0.3532 | 0.3163 | 0.3439 |
| 1 | 0.2880 | 0.3189 | 0.2927 | 0.1599 | 0.3075 | 0.3401 | 0.2976 | 0.3399 |
この結果から次のことがわかりました。
- ロジスティック回帰（Linear）は position 特徴量の利用で大きく指標が向上する
- 逆にXGBoostではこの手法は有効ではない
- ニューラルネットワークを使った手法では、バイアスを考慮しない single tower に比べて、バイアスを考慮したモデルが強い。
- 論文の主張であった、two tower モデル (PAL) は $w$ が大きい（relevance の交絡が強い）と性能が落ちるという点は再現できなかった。
- そもそも他の結果も元論文とは数字がかなり異なる。論文では人工クリックの生成・モデルの実装・ハイパーパラメータについて何も共有されていないのでこの辺りは仕方ない（もちろん自分の実装にバグがある可能性もある）。
なお、Debaised XGBoost は非常に悪い結果となりましたが、自分はこの方法が上手くいく場面を実務で見たことがあるので、データセットとの相性も大きいのではないかと思います。直感的には今回はポジションの影響が $1/p_i$ の形で入ってくるのでほとんどポジションで学習できてしまい、relevance 特徴をうまく学習できていないのだと思います。
さいごに
次は counterfactual 系の実用的な手法を調べて比較してみたいです。実装にバグを見つけたら、リポジトリで報告をして頂けると助かります。
自分で実験したところ、和の形の方が少しだけ性能が良かったです。
推薦の retrieval で使われる two-tower モデルとは異なります。
XGBoostには最近ポジションバイアス除去のオプションが追加されたらしく、lambdarank_unbiased=True で使えるようですが、試してみたところあまり効果はなかったです。ちゃんと内容を理解していないので比較対象からは抜いています。