NetflixのSequential ABテスト論文を読む

最近Netflixのテックブログを読んでいたらsequential AB testingについての話題があった。

Sequential A/B Testing Keeps the World Streaming Netflix Part 1: Continuous Data

Medium

Sequential Testing Keeps the World Streaming Netflix Part 2: Counting Processes

Medium

Sequential AB testing というのは、実験中に継続的にメトリクスを監視し、treatment と control で有意差が出た瞬間に実験を停止しようというものだ。もちろん、普通の t 検定やカイ二乗検定を実行すると大変な多重検定になるので、有意差が出やすくなってしまう (Type I errorが増加してしまう)。

そこで、実験のどの時刻でも、Type I errorが適切な制御下にあるような検定統計量を定義し、それに基づいて実験の早期打ち切りをできるようにしたというのが、冒頭のブログの趣旨である。これは論文になっていて、NeurIPSに採択もされたらしい。

Anytime-Valid Inference for Multinomial Count Data

arXiv.org

「有意差が出た瞬間に実験を打ち切って良い」というのは実務家としてはとても便利な性質なので、この論文をざっくり理解してみようと思い、このブログ記事を書いてみた。

検定統計量

今回対象とするのは離散的な「カウント」データである。例えば、ECサイトに何か新施策を実装してそれを treatment 群のユーザにだけ見えるようにし、サイトに訪問したユーザーが商品を購入したら、所属する群の conversion カウントが1インクリメントされるというような状況をイメージして欲しい。各時刻 $t$ で $\boldsymbol{n}_t = (n_{t,1}, n_{t,2}, \dots, n_{t,d}) $ という整数値のデータが得られる ($d$ は群の数で $n_{t,i}$ が群 $i$ でコンバージョンしたユーザー数)。

通常のABテストであれば、あらかじめ必要なサンプルサイズを見積り期間を定めて実験し、実験終了後に一度だけ検定を行う。今回のカウントデータであれば、カイ二乗検定がよく使われるだろう。¹

しかしここでは各時刻で毎回検定を行いたいのであった。上記論文に倣い、そのための検定統計量を構成しよう。

まず、帰無仮説 $M_0$ として以下のような多項分布から独立に生成される確率変数 $\boldsymbol{x}_i$ を考える \begin{align} \label{eq:eq-m0} \boldsymbol{x}_1, \boldsymbol{x}_2, \dots | M_0 \sim \mathrm{Multinomial(\boldsymbol\theta_0)} \end{align} $\boldsymbol{x}_i$ は one-hot ベクトル形式であり、$\sim$ は i.i.d であるとする。$\boldsymbol{x}_i$ を足すと上のカウント $\boldsymbol{n}_t$ になると思ってもらえれば良い。

次に対立仮説 $M_1$ を設定する。ここでは両側検定をすることにし $\boldsymbol\theta \neq \boldsymbol\theta_0$ となる生成過程として以下を考える \begin{align} \label{eq:eq-m1} \boldsymbol{x}_1, \boldsymbol{x}_2, \dots |\boldsymbol\theta ,M_1 &\sim \mathrm{Multinomial(\boldsymbol\theta)}\\ \notag \boldsymbol\theta &\sim \mathrm{Dirichlet}(\boldsymbol\alpha_0) \end{align} Dirchlet 分布は連続値の分布であり、特定の $\boldsymbol\theta=\boldsymbol\theta_0$ を取る確率はゼロなので、対立仮説になっている。

そして以下のベイズファクターを定義しよう²

\begin{align} \label{eq:eq-bf} O_n(\boldsymbol\theta_0)=BF_{10}(\boldsymbol{x}_{1:n})=\frac{p(\boldsymbol{x}_{1:n}|M_1)}{p(\boldsymbol{x}_{1:n}|M_0)} \end{align}

ベイズファクターについては以前も記事にしたが、ベイズ統計の枠組みで検定を行う手法の一つである。頻度論や、同じくベイズの枠組みでも信用区間を使った検定ではできないことができるので、使い勝手は良くないが場合によっては有用だという認識だったが、こういう使い道もあるようだ。

このベイズファクターを解析的に扱える形にしよう。周辺尤度の計算は初等的な積分をすればよく $\boldsymbol{x}_i$ の各成分を足したものを $S^n_i=\sum_{j=1}^nx_{j,i}$, $\boldsymbol{S}_n = (S^n_1, \dots, S^n_d)$ と書くと

\begin{align} \label{eq:eq-bf-calculated} O_n(\boldsymbol\theta_0)=\frac{\mathrm{Beta}(\boldsymbol{\alpha}_0 + \boldsymbol{S}_n)}{\mathrm{Beta}(\boldsymbol{\alpha_0})} \frac{1}{\boldsymbol\theta_0^{\boldsymbol{S}_n}} \end{align}

となることがわかる。$\mathrm{Beta}$ は $d$ 次元のベータ関数で、$\boldsymbol\theta_0^{\boldsymbol{S}_n}$ は成分ごとに冪乗して成分間で積を取った量である。

このベイズファクター $O_n(\boldsymbol\theta_0)$ は逐次検定をするのに望ましい性質を持っている。詳しい証明は自分の能力を超えるので書けないが、冒頭の論文によると $O_n(\boldsymbol\theta_0)$ が nonnegative supermartingale になることを利用すると以下の性質を示すことができるらしい:

性質: $O_n(\boldsymbol\theta_0) \geq 1/u$ となる $n$ が存在する確率は $u$ 以下である ($0\leq u \leq 1$)

そこでこのベイズファクターを利用した sequential p-value を

\begin{align} p_n = \mathrm{min}(p_{n-1}, 1/O_n(\boldsymbol{\theta}_0)),\text{ w/ } p_0=1 \end{align}

として定義すると

性質: $p_n\leq u$となる $n$ が存在する確率は $u$ 以下である ($0\leq u \leq 1$)

を持つことがわかる。

確かにこれは直感的に「普通の」p-value の拡張と思える。もし、ある時刻 $n$ で $p_n > u$ になったとすれば、それは帰無仮説の下では確率 $u$ 以下でしか起こらない稀な事象が起こったということであり、検定の文脈では背理法的に帰無仮説を棄却することになる。

ベルヌーイ過程などへの応用

以上は多項分布を生成する過程 \eqref{eq:eq-m0} や \eqref{eq:eq-m1} の話なので、一見すると使い道は限られるが、冒頭に述べた例のようにメトリクスをカウントデータとして読み替えることができれば広く適用できる。

もう少し具体的に、はじめに述べたコンバージョン有無を集計するABテストを考えよう。$\boldsymbol{x}_n$ を $n$ 番目のコンバージョンがどの群で発生したかを表すものとする。例えば $\boldsymbol{x}_3 = (0, 1, 0)$ であれば3番目のコンバージョンが群2で発生したということである。群 $i$ におけるコンバージョン確率を $p_i$, また各ユーザーの群 $i$ への割り当て確率を $\rho_i$ とすると、次のコンバージョンがどの群で起こるかを表す確率は

\begin{align} \theta_i = \frac{\rho_i p_i}{\sum_{j=1}^d \rho_i p_i} \end{align} とかける。帰無仮説は群ごとのコンバージョン確率 $p_i$ が全て等しいとするので、結局 $\boldsymbol\theta_0=\boldsymbol\rho$ として、上の話を適用すれば良いことになる。ポアソン過程についても同様に考えられるので、冒頭の論文を読んでほしい。

ちなみにこの表式から、$p_i$ が群の割り当てと独立な時間依存性を持っていても問題なく適用できることがわかる。Netflixの実験では、コンバージョン確率が実験中に時間変化することがあると報告されている。

シミュレーション

ベルヌーイ過程をシミュレーションして上記の手法を適用してみよう。実験に使ったノートブックは以下に上げた。

Sequential AB testing

Gist

Sequential p-value の計算はシンプルで、各時刻のカウントデータに対して式 \eqref{eq:eq-bf-calculated} で $\boldsymbol\theta_0=\boldsymbol\rho$ としたものを計算していくだけである。ただし prior のパラメータ $\boldsymbol{\alpha}_0$ には自由度がある。論文では、帰無仮説からズレるとしてもそのズレは小さいだろうとして、$\boldsymbol{\alpha}_0 = k \boldsymbol{\theta}_0$ を採用している ($k$ は大きい正の数）。³

Pythonで書くと以下のようになる ⁴

from scipy.special import loggamma, xlogy
import numpy as np

def sequential_p_value(counts, assignment_probabilities, k=100):
    counts = np.array(counts)
    assignment_probabilities = np.array(assignment_probabilities)
    dirichlet_alpha = k * assignment_probabilities

    log_bf = (
        loggamma(dirichlet_alpha + counts).sum() - loggamma((dirichlet_alpha + counts).sum())
        - loggamma(dirichlet_alpha).sum() + loggamma(dirichlet_alpha.sum())
        - np.sum(xlogy(counts, assignment_probabilities))
    )

    return min(1, np.exp(-log_bf))

ベータ関数はガンマ関数を使ってかけるのと、値が大きくなるのでできるだけ対数で計算しておくことがポイント。

二群のAAテスト ($\boldsymbol{p} = (0.5. 0.5)$) をして p-value の分布を見てみる。各群に割り当てられる確率は同じ ($\boldsymbol\rho=(0.5,0.5)$) とする。$n=4000$ まで取るシミュレーションを1000回繰り返し、上記の sequential p-value とカイ二乗検定を逐次行った結果を比較する。カイ二乗検定は各時刻で p-value を計算して最小値を保持するという、わざと不適切なやり方で行なった。

以下はその分布である。カイ二乗検定は明らかに p-value が0に寄ってしまっているのに対し、sequential p-value は概ね理想である一様に近い（少し1に偏っているのが気になるが…）。

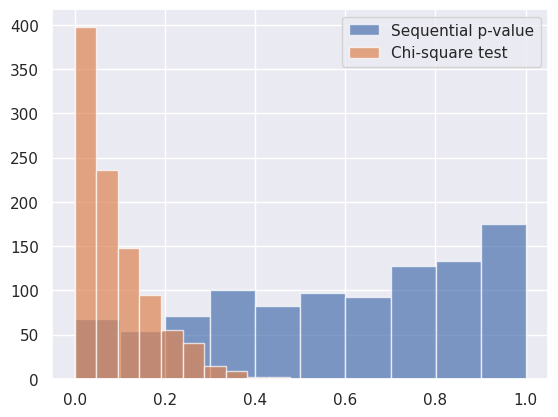
両者のType I errorの割合を有意水準 $0.05$ で計算してみると

• カイ二乗検定: 0.032
• Sequential p-value: 0.41

となり、カイ二乗検定は明らかに多重検定で Type I error が増幅されているのに対し、sequential p-value では適切に制御されていることがわかる。Sequential p-value の $p_n \leq u$ という性質はあくまで不等式なので、ピッタリ0.05 にはなっていないようだ。

上記の結果だけみると非常に便利で普通の検定より便利なのではと思ってしまうが、多重検定に対して頑健ということは、逆に検出力は低いのではないかという懸念が生じる。そこで $\boldsymbol{p} = (0.54. 0.5)$ と二群に差があるケースで同様にシミュレーションしてみた。ただし今回は多重検定にならないよう、カイ二乗検定では $n=4000$ で一回だけ p-value 計算をしている。この時、有意 ($p < 0.05$) になったものの割合は

• カイ二乗検定: 0.715
• Sequential p-value: 0.202

となった。やはり、検出力は低くなる傾向にあるようだ。

その他、実務のABテストではゼロイチの統計量ではなく連続値に対して t 検定を行うこともよくあるが、その場合には使えないし、カウントに対するモデリングになっているので単純な拡張も難しそうだと思う。

---